Delphi FAQ - Часто задаваемые вопросы
| Базы данных |
Графика и Игры |
Интернет и Сети |
Компоненты и Классы |
Мультимедиа |
|
ОС и Железо |
Программа и Интерфейс |
Рабочий стол |
Синтаксис |
Технологии |
Файловая система |
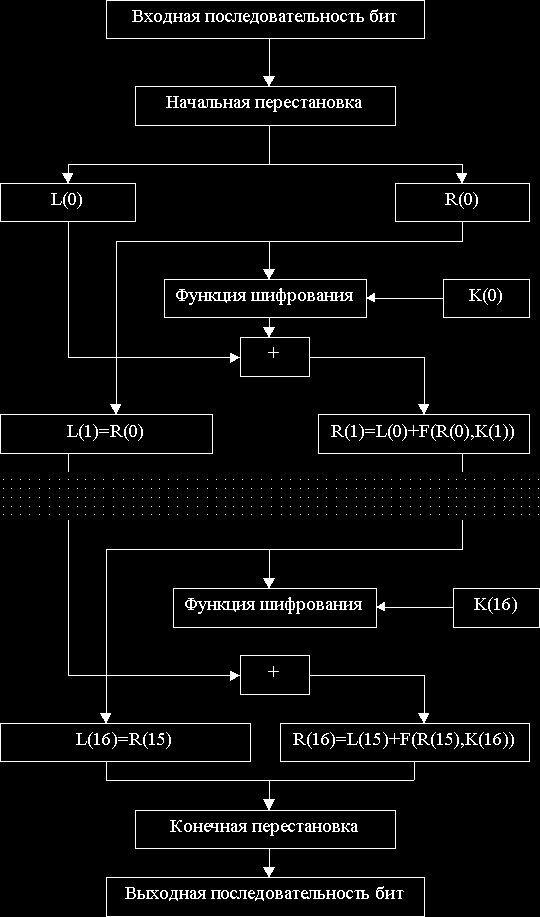
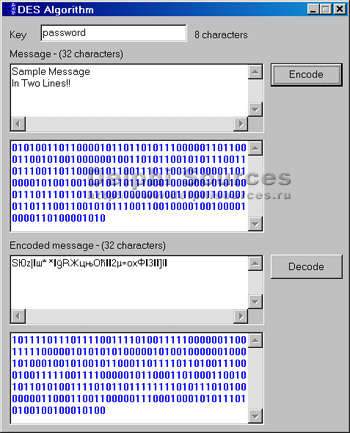
Алгоритм шифрования DESАлгоритм шифрования данных DES разработан для зашифрования и расшифрования данных разрядностью 64 бит на основе 64-битового ключа. Расшифрование выполняется по тому же ключу, что и зашифрование, но этот процесс является инверсным по отношению к процессу зашифрования данных. При описании алгоритма шифрования используются следующие обозначения. Если L и R - последовательности бит, то через LR будем обозначать конкатенацию последовательностей L и R, т.е. последовательность бит, размерность которой равна сумме размерностей L и R. В этой последовательности биты последовательности R следуют за битами последовательности L. Конкатенация битовых строк является ассоциативной, то есть запись ABCDE, означает, что за битами последовательности A, следуют, биты последовательности B, затем C и т.д. Символом + будем обозначать операцию побитового сложения по модулю 2. Процесс шифрования. Процесс шифрования данных поясняется рисунком 1. Сначала 64 бита входной последовательности перестанавливаются в соответствии с таблицей 1. Таким образом, бит 58 входной последовательности становится битом 1, бит 50 – 2 и т.д. Таблица 1. "Начальная перестановка"
Полученная последовательность бит разделяется на две последовательности: L(0) (биты 58, 50, 42, ..., 8) и R(0) (биты 57, 49, 41, ..., 7), каждая из которых содержит 32 бита. Затем выполняется итеративный процесс шифрования, который описывается следующими формулами: L(i)=R(i-1), i=1,2,...,16. R(i)=L(i-1) + F(R(i-1),K(i)), i=1,2,...,16. Функция F называется функцией шифрования. Ее аргументами являются последовательность R, полученная на предыдущем шаге, и 48-битовый ключ K(i), который является результатом функции преобразования 64-битового ключа шифра. Подробно функция шифрования и алгоритм получения ключей K(i) описаны ниже. На последнем шаге итерации будут получены последовательности L(16) и R(16), которые конкатенируются в 64-х битовую последовательность R(16)L(16). Видно, что в полученной последовательности 64 бита, перестанавливаются в соответствии с таблицей 2. Как легко видеть данная перестановка является обратной по отношению к начальной (см. таблицу 1). Таблица 2. "Конечная перестановка"
Полученная последовательность из 64 бит и будет являться зашифрованной последовательностью. Рисунок 1.
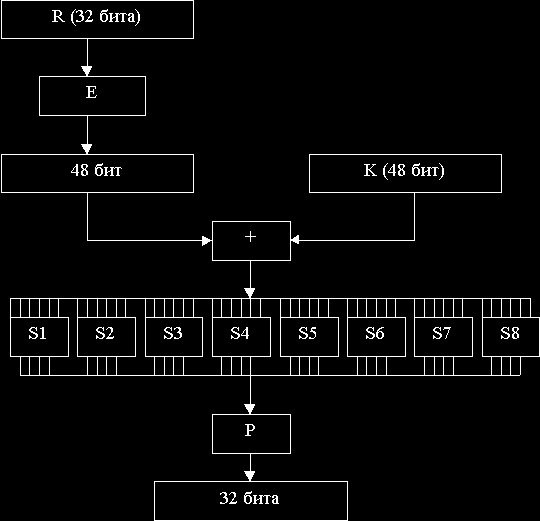
Процесс расшифрования. Процесс расшифрования данных является инверсным по отношению к процессу шифрования. Все действия должны быть выполнены в обратном порядке. Это означает, что расшифровываемые данные сначала переставляются в соответствии с таблицей 1, а затем над последовательностью бит R(16)L(16) выполняется те же действия, что и в процессе зашифрования, но в обратном порядке. Итеративный процесс расшифрования описан следующими формулами: R(i-1)=L(i), i =16, 15, ..., 1 L(i-1)=R(i)+F(L(i),K(i)), i=16, 15, ..., 1. На последнем шаге итерации будут получены последовательности L(0) и R(0), которые конкетанируются в 64 битовую последовательность L(0)R(0). В полученной последовательности 64 бита перестанавливаются в соответствии с таблицей 2. Результат преобразования - исходная последовательность бит (расшифрованное 64-битовое значение). Функция шифрования. Функция шифрования F(R,K) схематически показана на рисунке 2. Для вычисления значения функции F используется функция E (расширение 32 бит до 48), функции S(1), S(2),...,S(8) преобразование 6-битового числа в 4-битовое) и функция P (перестановка бит в 32-битовой последовательности). Приведем определения этих функций. Аргументами функции шифрования являются R (32 бита) и K (48 бит). Результат функции E(R) есть 48-битовое число, которое складывается по модулю 2 с числом K. Таким образом, получается 48-битовая последовательность, которая рассматривается, как конкатенация 8 строк длиной по 6 бит (т.е. B(1)B(2)B(3)B(4)B(5)B(6)B(7)B(8)). Результат функции S(i)B(i) - 4 битовая последовательность, которую будем обозначать L(i). В результате конкетанации всех 8 полученных последвательностей L(i) имеем 32-битовую последовательность L=L(1)L(2)L(3)L(4)L(5)L(6)L(7)L(8). Наконец, для получения результат функции шифрования надо переставить биты последовательности L. Для этого применяется функция перестановки P(L). Рисунок 2.
Функция расширения Е, выполняющая расширение 32 бит до 48, определяется таблицей 3. В соответствии с этой таблицей первые три бита Е(R) - это биты 32,1 и 2, а последние - 31,32,1. Таблица 3. "Функция расширения Е"
Функция S(i), которая преобразует 6-битовые числа в 4-битовые, определяется в таблицей 4. Таблица 4. "Функции преобразования S(i)" S(1)
S(2)
S(3)
S(4)
S(5)
S(6)
S(7)
S(8)
К таблице 4 требуются дополнительные пояснения. Каждая из функций S(i)B(i) преобразет 6-битовый код в 4-битовый выход по следующему алгоритму:
Предположим, что B=011011. Тогда S(1)(B)=0101. Действительно, k=1, l=13. В колонке 13 строки 1 задано значение 5, которое и является значением функции S(1)(011011). Функция перестановки бит P(L), также используемая для определения функции шифрования, задается значениями, приведенными в таблице 5. В последовательности L 32 перестанавливается так, чтобы бит 16 стал первым битом, бит 7 - вторым и т.д. Таблица 5. "Функция перестановки P"
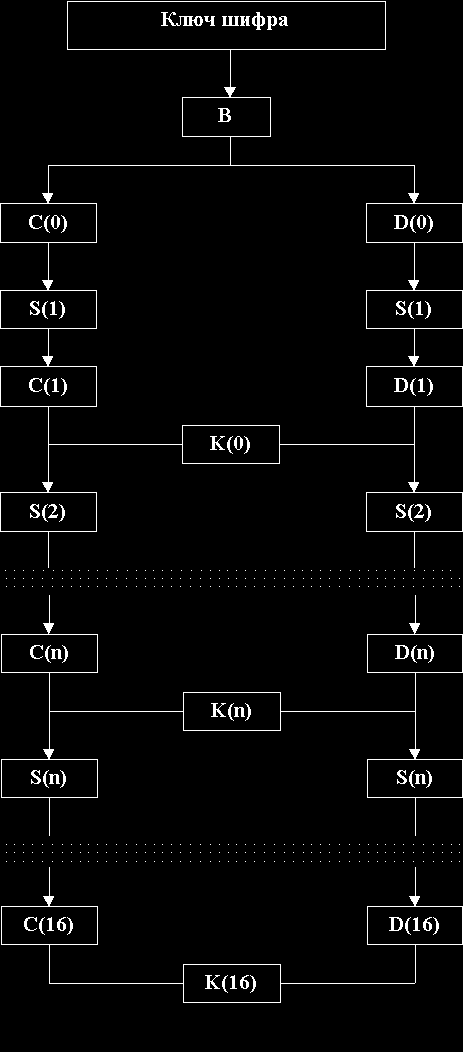
Процесс получения ключей. Чтобы завершить описание алгоритма шифрования данных, осталось привести алгоритм получение ключей K(i), i=1,2,...,16, размерностью в 48 бит. Ключи K(i) определяются по 64-битовому ключу шифра как это показано на рисунке 3. Рисунок 3.
В начале над ключом шифра выполняется операция B, которая сводится к выбору определенных бит и их перестановке, как это показано в таблицей 6. Причем, первые четыре строки определяют, как выбираются биты последовательности C(0) (первым битом C(0) будет бит 57 бит ключа шифра, затем бит 49 и т.д., а последними битами биты 44 и 36 ключа шифра), а следующие четыре строки - как выбираются биты последовательности D(0) (т.е. последовательность D(0) будем состоять из битов 63,55,...,12, 4 ключа шифра). Таблица 6. "Функция перестановки и выбора последовательности B"
Как видно из таблицы 6, для генерации последовательностей C(0) и D(0) не используются биты 8,16,25,32,40,48,56 и 64 ключа шифра. Эти биты не влияют на шифрование и могут служить для других целей (например, для контроля по четности). Таким образом, в действительности ключ шифра является 56-битовым. После определения C(0) и D(0) рекурсивно определяются C(i) и D(i), i=1,2,...,16. Для этого применяются операции сдвига влево на один или два бита в зависимости от номера шага итерации, как это показано в таблицей 7. Операции сдвига выполняются для последовательностей C(i) и D(i) независимо. Например, последовательность C(3) получается, посредством сдвига влево на две позиции последовательности C(2), а последовательность D(3) - посредством сдвига влево на две позиции последовательности D(2). Следует иметь в виду, что выполняется циклический сдвиг влево. Например, единичный сдвиг влево последовательности C(i) приведет к тому, что первый бит C(i) станет последним и последовательность бит будет следующая: 2,3,..., 28,1. Таблица 7. "Функция сдвига Si"
Ключ K(i), определяемый на каждом шаге итерации, есть результат выбора определенных бит из 56-битовой последовательности C(i)D(i) и их перестановки. Другими словами, K(i) = K(C(i)D(i)), где функция K определяется данными, приведенными в таблицей 8. Таблица 8. "Функция перестановки и выбора K"
Как следует из таблицы 8 первый бит K(i) - это бит 14 последовательности C(i)D(i), второй - бит 17, последний - бит 32. |
Похожие по теме исходники |
Copyright © 2004-2024 "Delphi Sources" by BrokenByte Software. Delphi World FAQ