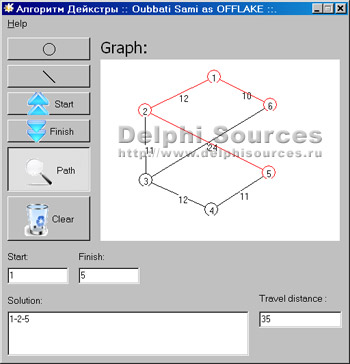
Алгоритм обхода препятствий

Автор: Алексей Моисеев

Предлагаемый алгоритм обхода препятствий - это, так называемый, обобщенный алгоритм Дейкстры. В англоязычной литературе он называется алгоритмом A*.

Реализация алгоритма: скачать проект (191 К)

1. Карта разбита на квадратные части, назовем их клетками.
2. Каждая клетка имеет несколько показателей:
- 1) стоимость прохождения по этой клетке,
- 2) предыдущая клетка - клетка из которой пришли в эту клетку,
- 3) статус клетки (непосещенная, граничная, отброшенная),
- 4) оценка пройденного пути,
- 5) оценка оставшегося пути.
3. Имеется две клетки - начальная и конечная.
4. Сосед клетки - клетка в которую можно попасть из рассматриваемой за 1 шаг.

Общий принцип: на каждой итерации из всех граничных точек выбирается та, для которой сумма уже пройденного пути и пути до конца по прямой является минимальной, и от нее осуществляется дальнейшее продвижение.

Алгоритм этот проще реализовать, чем описать:

Start - начальная клетка
Finish - конечная клетка.
Алгоритм итерационный
1 шаг: Помечаем Start как граничную точку.
2 шаг: Среди всех граничных точек находим Клетку1 - клетку с минимальной суммой оценки пройденного пути g и оценки оставшегося пути h.
3 шаг: Для Клетки 1 рассматриваем соседей. Если сосед имеет статус непосещенного, то мы обозначаеми его как граничную клетку, и указываем Клетку1 как предыдущую для него. Оценку g1 для соседа принимаем равной g+p, где p-стоимость прохождения по клетке сосед, а g - оценка пройденного пути для Клетки1 . Оценка h для любой клетки равна длине кратчайшего пути (по прямой от рассматриваемой клетки до клетки Finish) Рассматриваемую Клетку1 помечаем как отброшенную.
4 шаг: Если на предыдущем шаге один из соседей оказался равен клетке Finish, то путь найден. Если ни одного нового соседа не существует, то нет и пути.
5 шаг: Переход на шаг 2.

Буду рад любым предложениям по оптимизации, так как меня, к сожалению, не устраивает быстродействие.

Недавно добавленные исходники
• DeLiKaTeS Tetris (Тетрис) 158 • TDictionary Custom Sort 3 335 • Fast Watermark Sources 3 086 • 3D Designer 4 845 • Sik Screen Capture 3 339 • Patch Maker 3 551 • Айболит (remote control) 3 656 • ListBox Drag & Drop 3 013 • Доска для игры Реверси 81 689 • Графические эффекты 3 943 • Рисование по маске 3 247 • Перетаскивание изображений 2 627 • Canvas Drawing 2 750 • Рисование Луны 2 578 • Поворот изображения 2 187 • Рисование стержней 2 168 • Paint on Shape 1 568 • Генератор кроссвордов 2 235 • Головоломка Paletto 1 767 • Теорема Монжа об окружностях 2 229 • Пазл Numbrix 1 685 • Заборы и коммивояжеры 2 057 • Игра HIP 1 282 • Игра Go (Го) 1 230 • Симулятор лифта 1 475 • Программа укладки плитки 1 216 • Генератор лабиринта 1 548 • Проверка числового ввода 1 365 • HEX View 1 497 • Физический маятник 1 358

Алгоритм обхода препятствий

Похожие по теме исходники